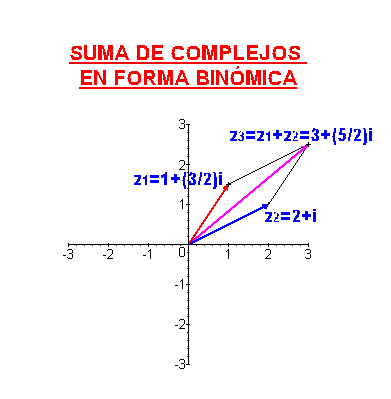
(1 + 3/2 i) + (2 + i) = 5 + 5/2 i
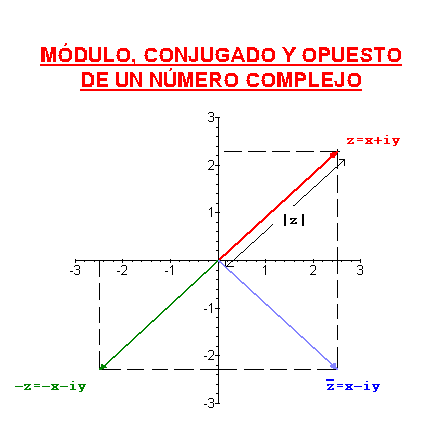
se define el módulo de un número complejo como el módulo del vector que lo representa, es decir, si 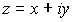 , entonces el módulo de
, entonces el módulo de  es
es 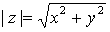 .
.
El conjugado de un número complejo se define como su simétrico respecto del eje real, es decir, si 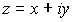 , entonces el conjugado de
, entonces el conjugado de  es
es 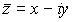 .
.
El opuesto de un número complejo es su simétrico respecto del origen.
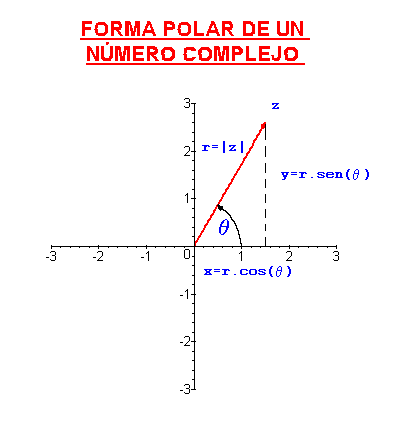
Forma polar o módulo-argumento
Otra forma de expresar un número complejo es la forma polar o forma módulo-argumento,
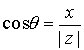 ,
, 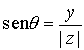 .
.
Dos números complejos 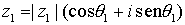 y
y 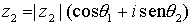 , representados en forma polar son iguales si y sólo si sus módulos son iguales
, representados en forma polar son iguales si y sólo si sus módulos son iguales 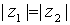 , y sus argumentos se diferencian en un número entero de vueltas, es decir,
, y sus argumentos se diferencian en un número entero de vueltas, es decir, 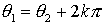 , con
, con 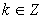 .
.
La forma polar de un número complejo es especialmente cómoda a la hora de multiplicar, ya que basta con multiplicar los módulos y sumar los argumentos, es decir, si 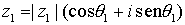 , y
, y 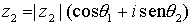 , entonces
, entonces
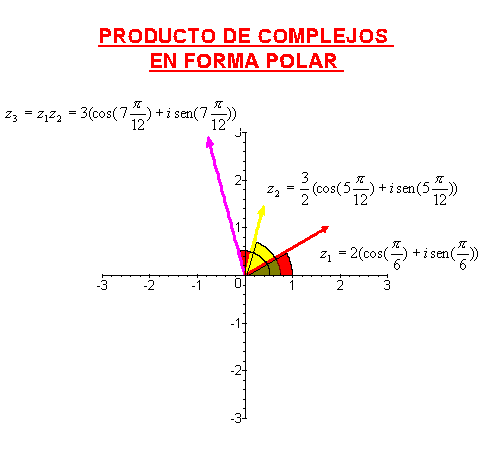
Del mismo modo se puede calcular el cociente de un complejo por otro no nulo sin más que dividir los módulos y restar los argumentos:
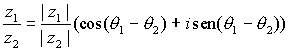 ,
,siempre que 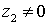 .
.
Una variante de la forma polar se obtiene al tener en cuenta la conocida como fórmula de Euler:
para 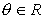 .
.
Esto nos permite escribir un número complejo en la forma siguiente, denominada forma exponencial:
Esta nueva forma es especialmente cómoda para expresar productos y cocientes ya que sólo hay que tener en cuenta las propiedades de la función exponencial (para multiplicar se suman exponentes y para dividir se restan). En particular, para potencias con exponentes enteros se tiene 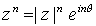 .
.
Esto nos permite dar una nueva expresión para el inverso de un complejo no nulo en la forma 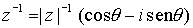 .
.
Estudiemos ahora las potencias con exponente racional de un número complejo. Dado 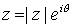 , sea
, sea 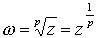 , para un número natural p.
, para un número natural p.
Si 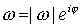 , puesto que
, puesto que 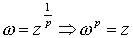 , es decir,
, es decir, 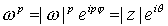 . Por tanto,
. Por tanto, 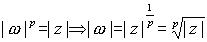 , y además,
, y además, 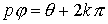 , o sea,
, o sea, 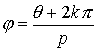 , para
, para 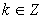 .
.
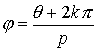 , para
, para De todos estos valores sólo p consecutivos son distintos, el resto resulta ser repetición sucesiva de valores ya obtenidos. Por tanto, un número complejo tiene siempre p raíces p-ésimas distintas
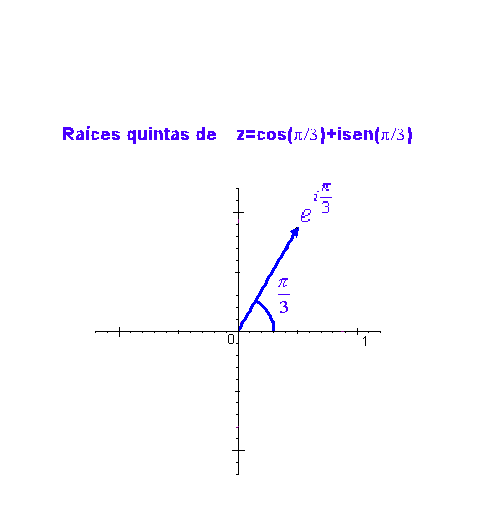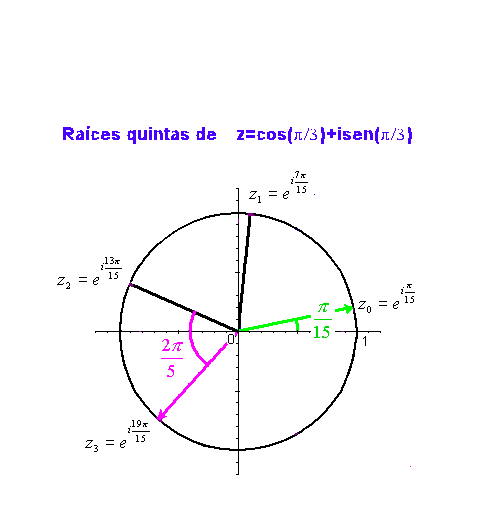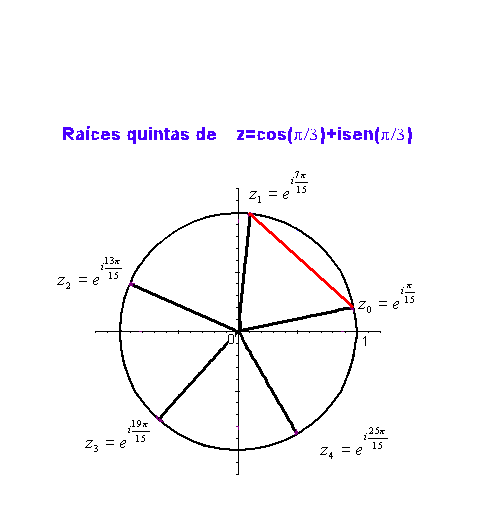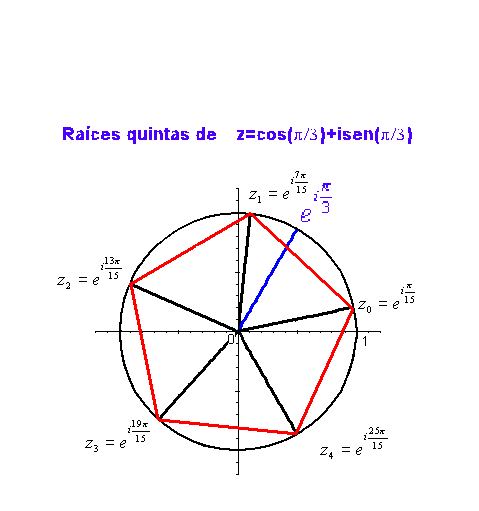
Se puede observar que las p raíces pésimas tienen todas el mismo módulo, y sus argumentos se diferencian en 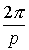 cada uno del siguiente, esto es, las raíces p-ésimas se encuentran en los vértices de un polígono regular de p lados incrito en la circunferencia de centro 0 y radio
cada uno del siguiente, esto es, las raíces p-ésimas se encuentran en los vértices de un polígono regular de p lados incrito en la circunferencia de centro 0 y radio 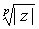 .
.
Como ejemplo, en la siguiente gráfica podemos ver las raíces quintas de 

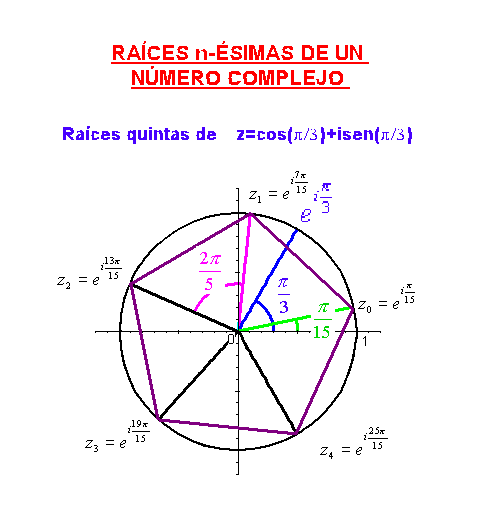
No hay comentarios:
Publicar un comentario